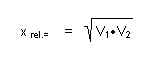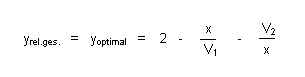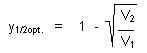"Die Arbeitsteilung ist keine Erfindung der Menschen"- Adam Smith.
Schon
Milliarden Jahre vor der Entdeckung der Formel E=mc2 und durch Menschen
ausgelöste atomare Kernreaktionen haben chemische Verbindungen ein
gegenteiliges kettenreaktives Prinzip entdeckt,
nämlich das der Zellteilung.
Innerhalb einzelliger Lebensformen wurde bereits zuvor schon durch Photosynthese aus Sonnenlicht Energie gewonnen und durch Arbeitsteilung zwischen ihren Zellorganellen der Energieverbrauch der Zelle minimiert.
Ihre einfache Form der Energieeinsparung ist die durch arbeitsteilige Zweiteilung, deren optimale
Verteilung sich allgemein primal so darstellen
lässt:
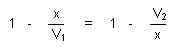 |
Dieses wichtige auch in dualer Form entscheidende Prinzip der Energieeinsparung lebender Strukturen könnte anscheinend eine Reaktion auf unsere durch große Temperaturschwankungen geprägte aber langfristig unaufhaltsam abkühlende Erde sein.
Arbeitsteiliges Leben contra Entropie?
Doch
ist mittlerweile die Vielfalt arbeitsteilig entwickelten Lebensformen
unübersehbar
groß geworden.
Wenn also nach grundlegenden und damit auch mathematischen Gesetzen der
Arbeitsteilung gesucht wird, sollte sinnvoller Weise mit der
einfachsten Möglichkeit der Zweiteilung
einer Arbeit zwischen zwei relativ
selbständigen Wirtschaftseinheiten
begonnen werden.
Das
duale Ziel dieser zweiseitigen
arbeitsteiligen Optimierung ist die Minimierung des Aufwands -
also letztlich Energieeinsparung.
Bei Verallgemeinerung und Formulierung stellt sich dann heraus, dass letztlich nur das Verhältnis der beiden Verhältnisse (V1 und V2) des ursprünglichen Aufwandes die Größe der beidseitigen Einsparungen bestimmt.
Wer
Verteilungs-Gerechtigkeit in der arbeitsteiligen menschlichen
Gesellschaft anstrebt, sollte darum folgenden mathematischen Grundlagen
der Arbeitsteilung kennen: